Deep Learning approach of Quantum Monte Carlo Simulations

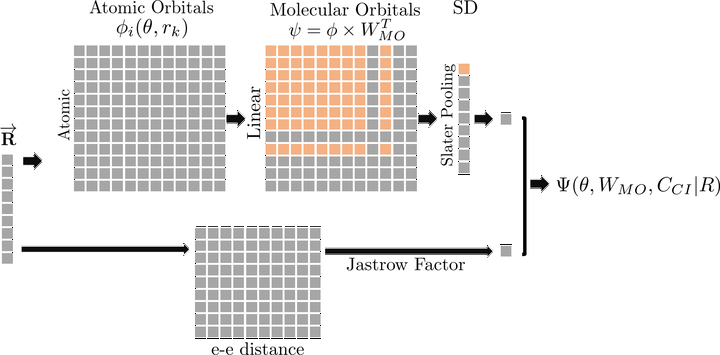
Quantum Monte Carlo (QMC) simulations hold great promises for exascale electronic structure calculations as the MCMC sampling can easily be distriubted on large scale compute infrastructure with minimal communication cost. QMC simulations consists of interleaed sampling and optimization of a wave function ususally expressed as :

$$\Psi(R) = J(R) \sum_n c_n D_n^\uparrow(Q) D_n^\downarrow(Q)$$

where $J(R)$ is a Jastrow factor capturing electronic correlation and $D_n^\uparrow(Q)$ and $D_n^\downarrow(Q)$ Slater determinants constructed over the basis of molecular orbitals and computed at the backflow-transformed coordinates, $Q$, of the spin up and down electrons.

The code we developped, QMCTorch, implement these wave function ansatz in a quantum aware neural network. Well known ingredients of the wave function, e.g. the atomic and molecular orbitals have been directly implemented in the architecture of the network. Other ingredients such a the Jastrow factor and the backflow transformation kernels can be defined as sub-network allowing for a very flexible functional form.

This semi-analytical wave function ansatz allows for fast calculations of the key observables, e.g. the kinetic energy and atomic forces, via the Jacobi Formula. For example in absence of backflow and Jastrow the kinetic energy can be evaluated with the help of :

$$\frac{\partial^2 \det{A}}{\partial x_i^2} = Tr(A^{-1} \frac{\partial^2 A}{\partial x_i^2})$$

Hence avoiding a costly computation of the diagonal Hessian via automatic differentiation.

QMCTorch